
Constructing Statistical
Tolerance Limits for
Non-Normal Data
Presented by
Dr. Neil W. Polhemus

Statistical Tolerance Limits
• Consider a sample of n observations taken from a
continuous population.
{X
1
, X
2
, …, X
n
}
• Statistical tolerance limits create an interval that
bounds a specified percentage of the population at a
given level of confidence.
(such as 99% of the population with 95% confidence)
• These intervals are often used to demonstrate
compliance with a set of requirements or
specification limits.
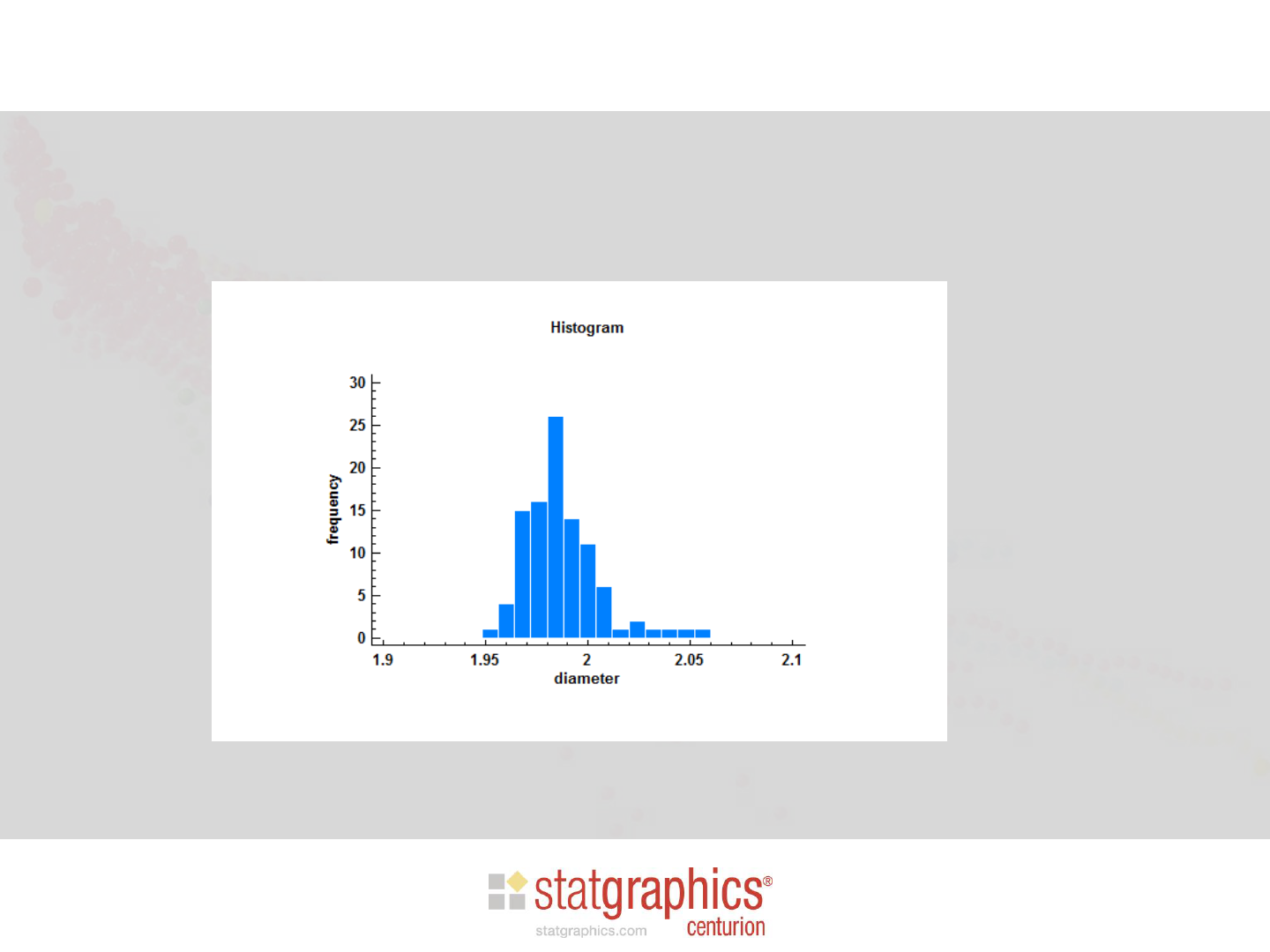
Example: Medical Devices
• Consider the following measurements of the diameter of
a sample n = 100 of medical devices:
• The specification limits are 2.0 ± 0.1

Assuming Normality
If we could assume that the data are a random
sample from a normal distribution, then a 95%
statistical tolerance interval for 99% of the
underlying population would be given by:
K depends on the level of confidence 100(1-a)%
and the percentage of the population P to be
bound.

General Approach for Constructing
Statistical Tolerance Limits
• Step 1: Test data for normality.
– If normal dist. is tenable, calculate normal tolerance limits.
• Step 2: If not normal, search for a normalizing transformation.
– If acceptable transformation is found, calculate normal
tolerance limits for transformed data and invert the limits.
• Step 3: If transformation approach fails, try alternative
distributions such lognormal, extreme value or Weibull.
– If a good fit is found, calculate tolerance limits using that
distribution.
• Step 4: If all else fails, calculate nonparametric tolerance
limits.
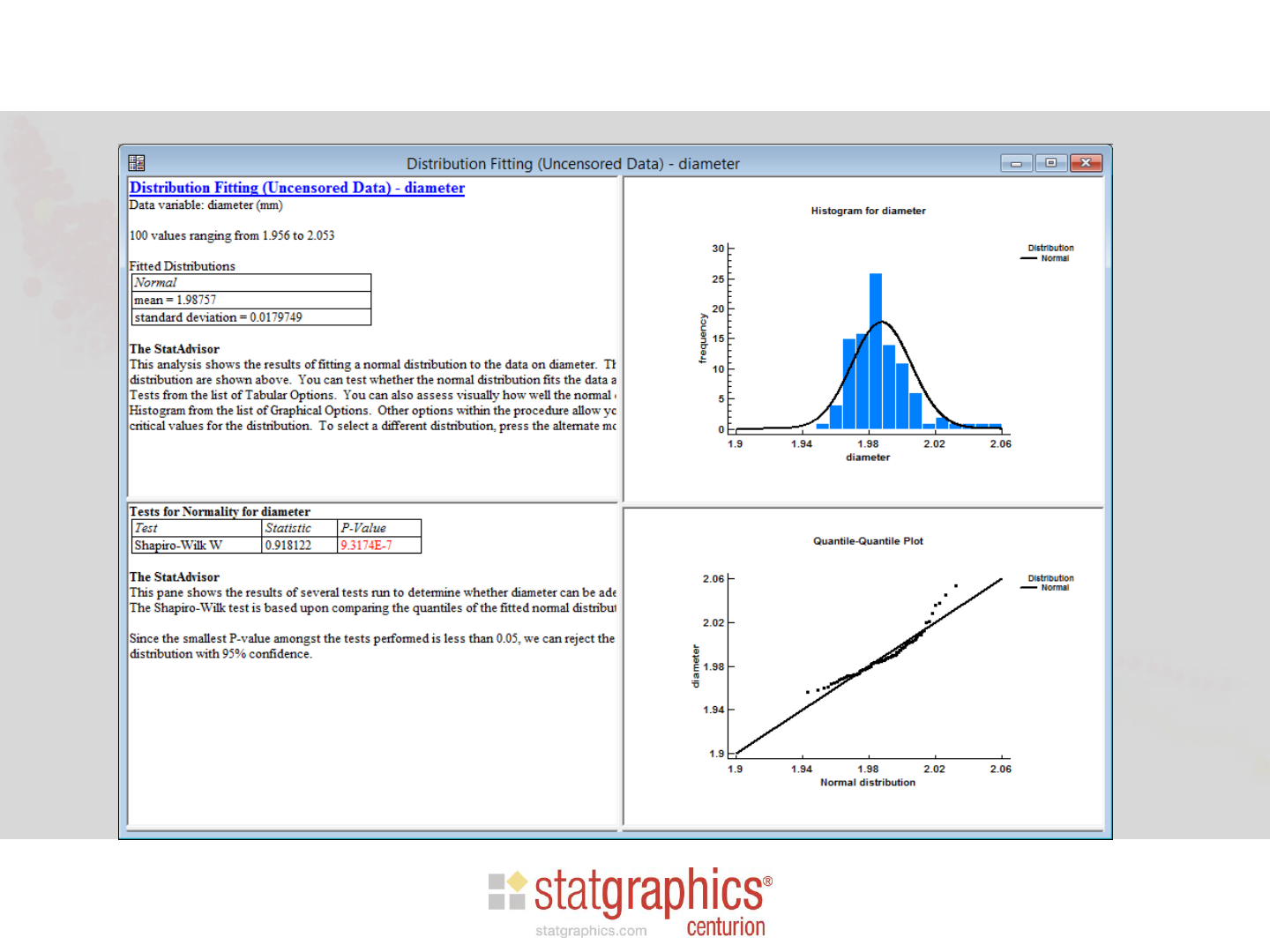
Step 1: Test for Normality

Tests for Normality
• Shapiro-Wilk test: recommended for sample
sizes between 3 and 5000.
• Anderson-Darling test: recommended for sample
sizes n > 5000.
• Chi-square test: recommended for heavily
rounded data. NOTE: be sure to set up classes
that match the rounding of the data.
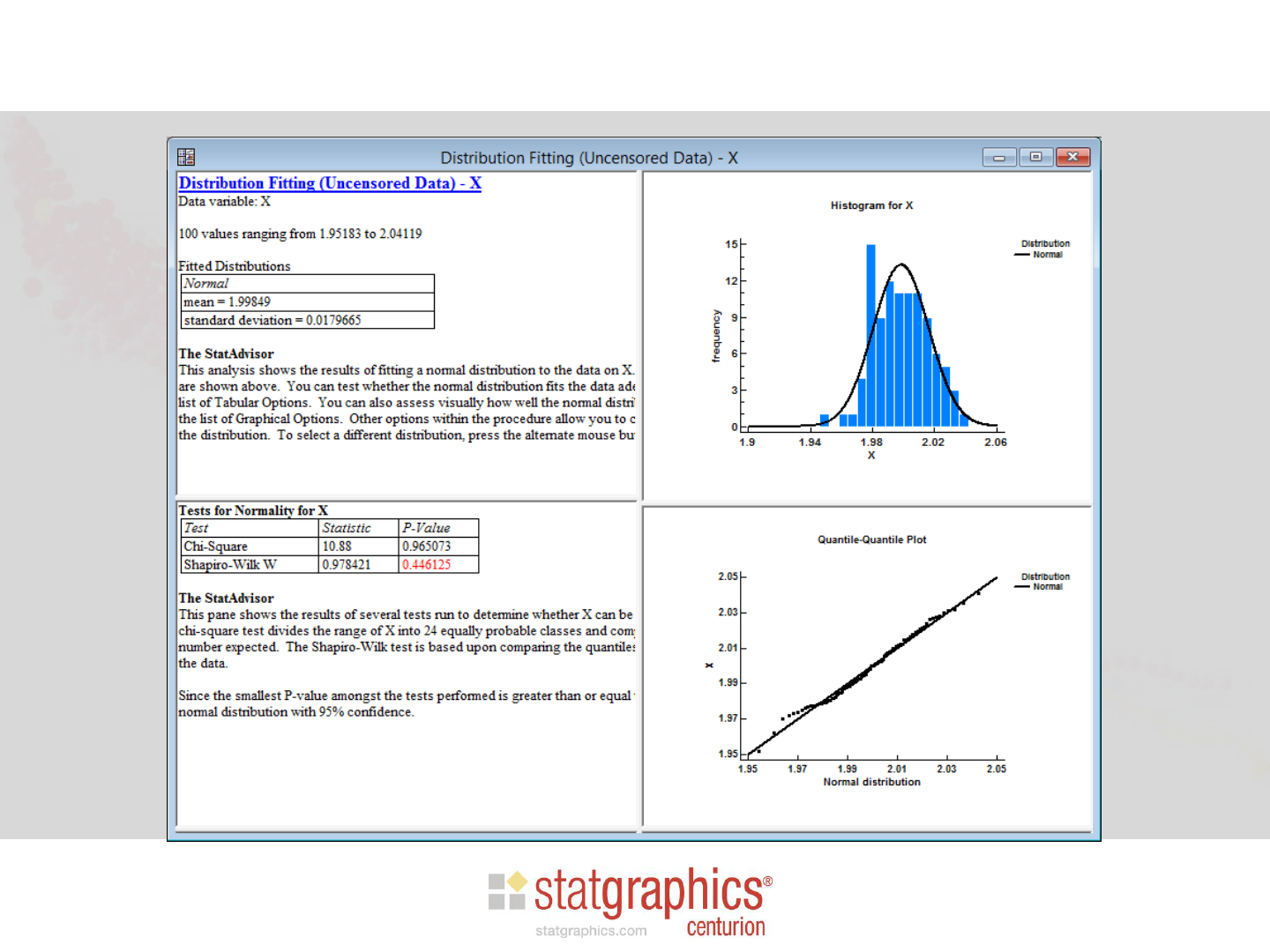
Warning: Beware of rounded data
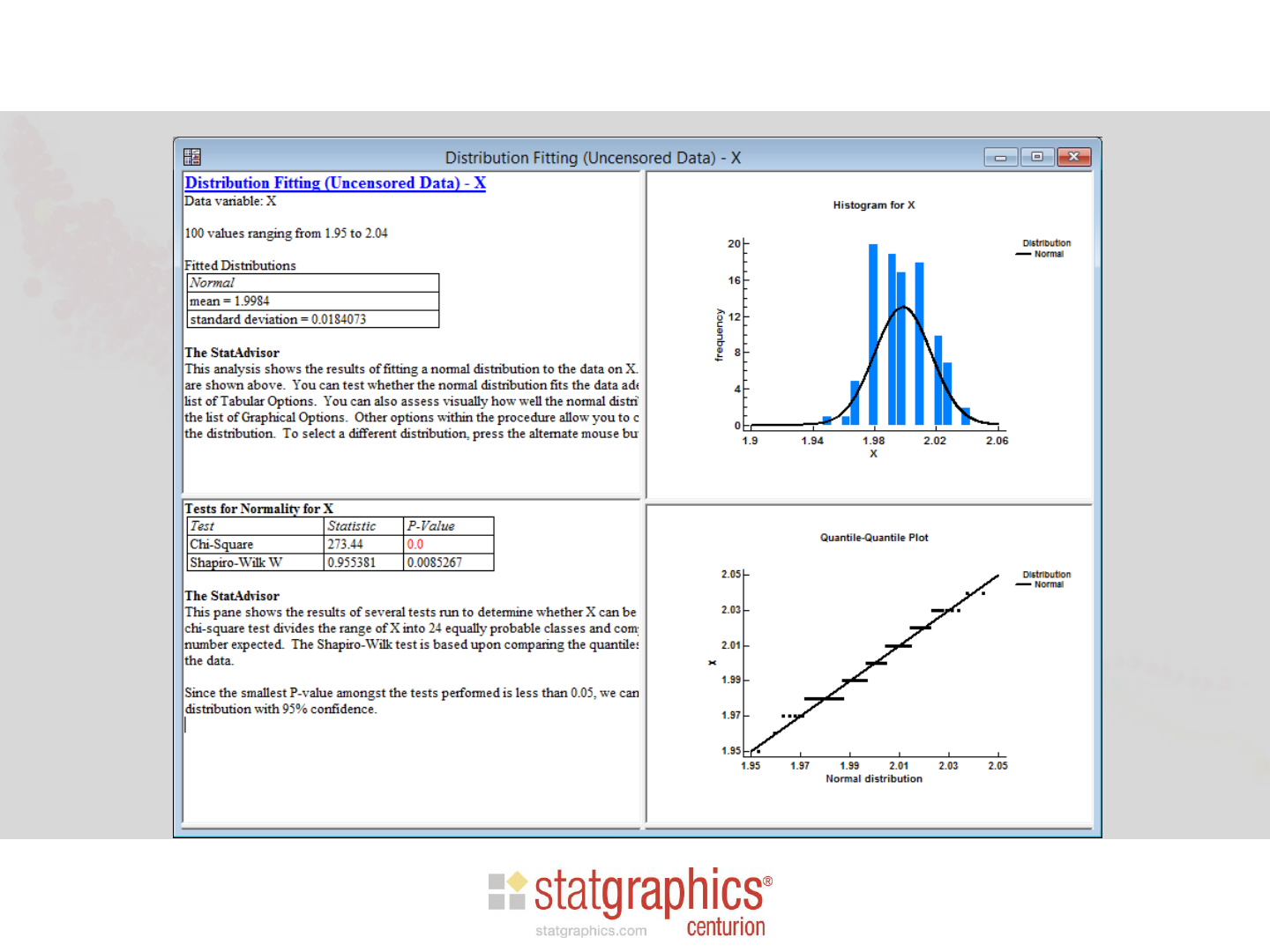
Warning: Beware of rounded data
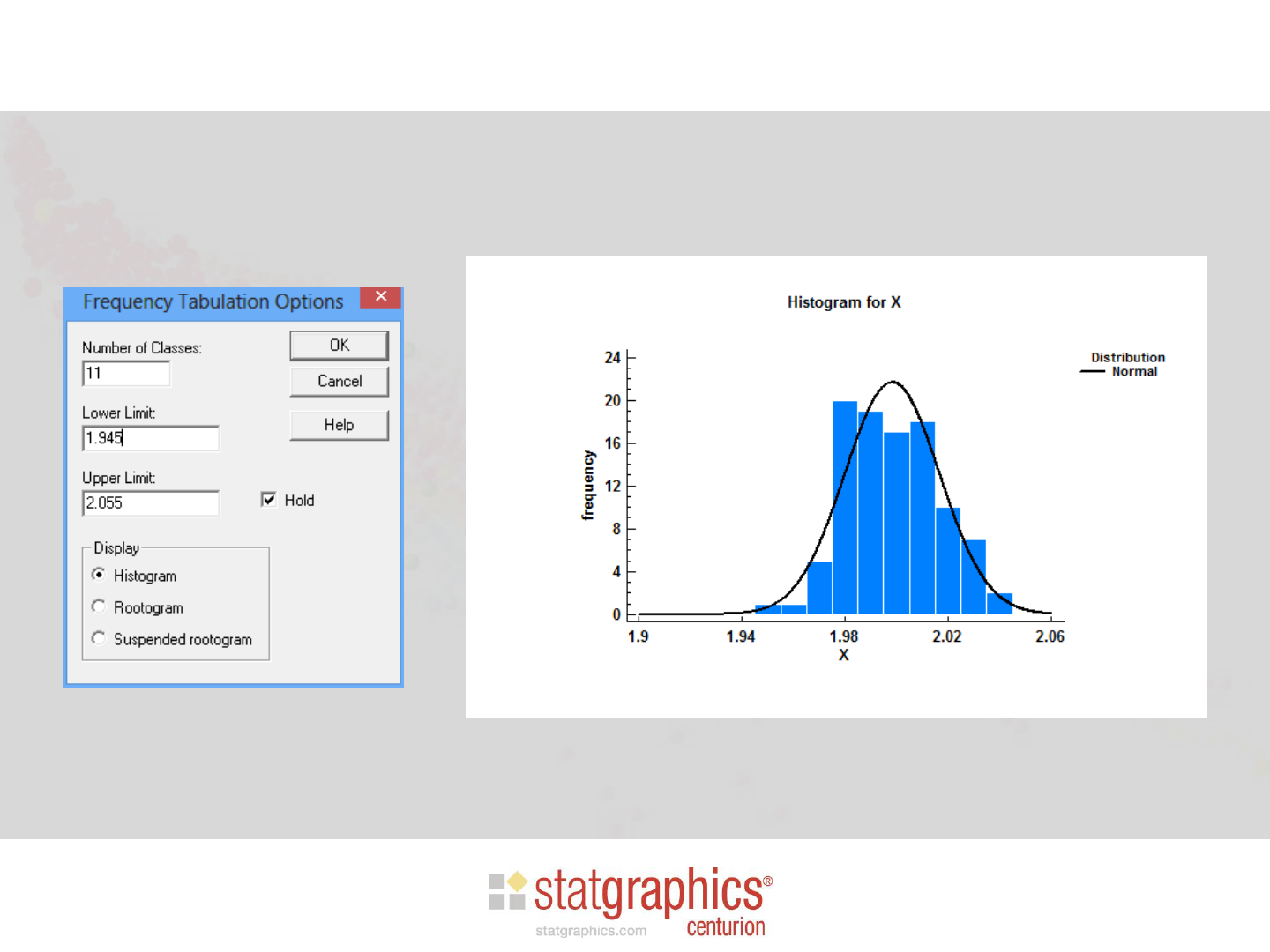
Solution: bin the data
• Be sure classes match the rounding
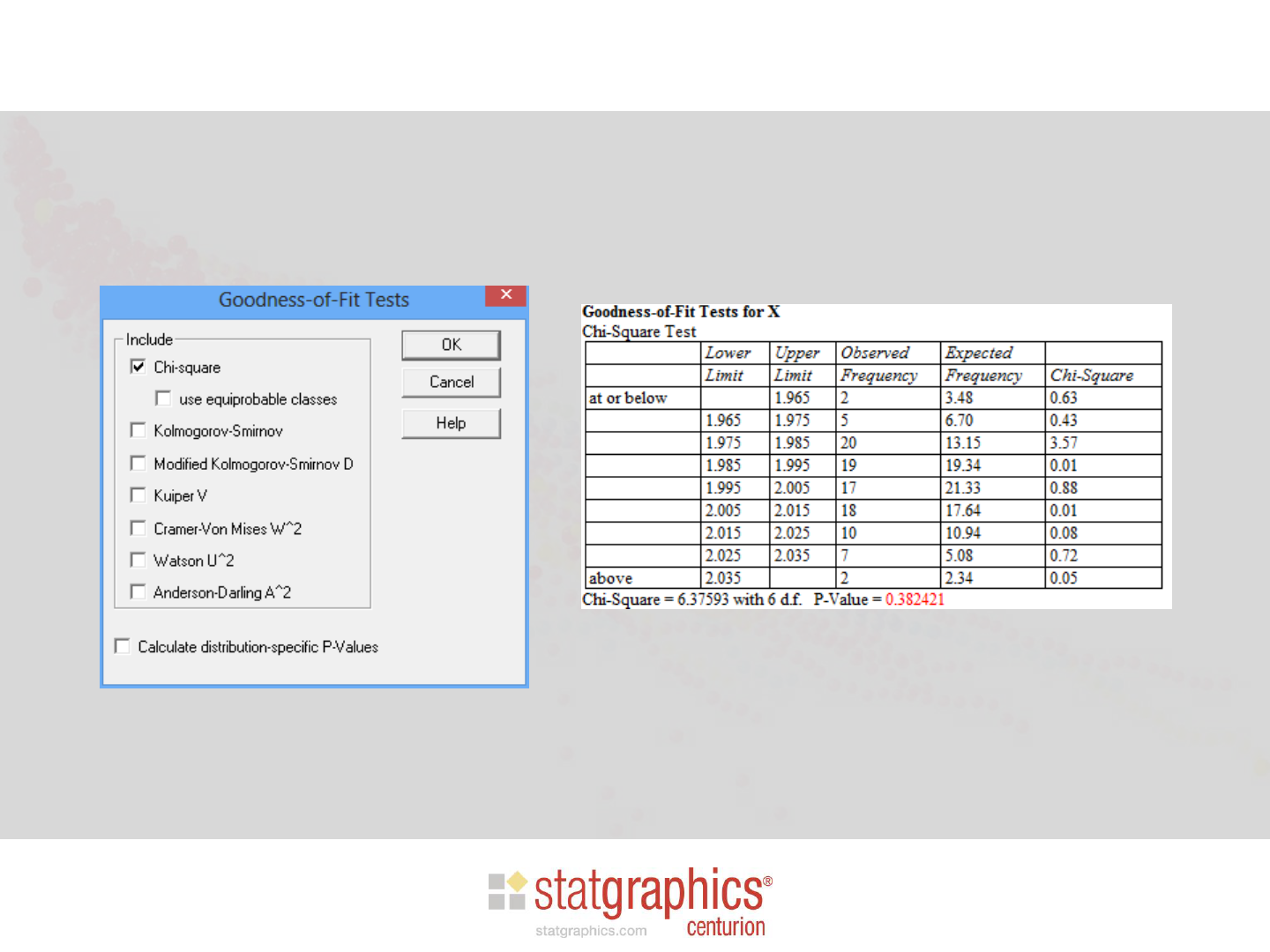
Run chi-square test

Step 2: Search for normalizing transformation
• If X does not follow a normal distribution, it may
be possible to find a power p such that X
p
is
normally distributed.
• If so, normal tolerance limits may be constructed
for X
p
and then inverted to create limits for X.
• The general method of Box and Cox may be
used to find the best value of p.
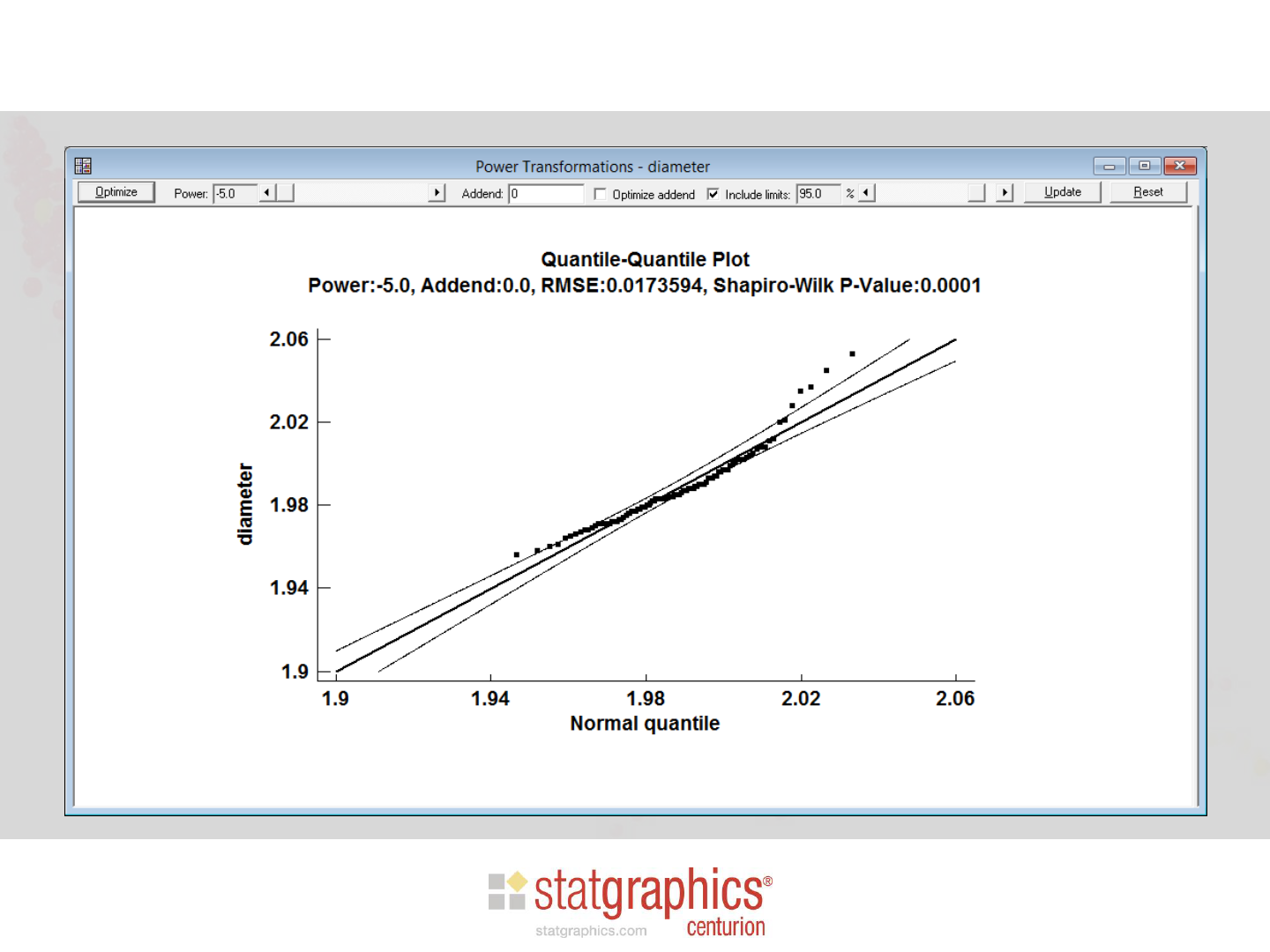
Statlets - Power Transformations

Power plus Addend
• If a simple power transformation does not work,
an addend can be estimated as well:
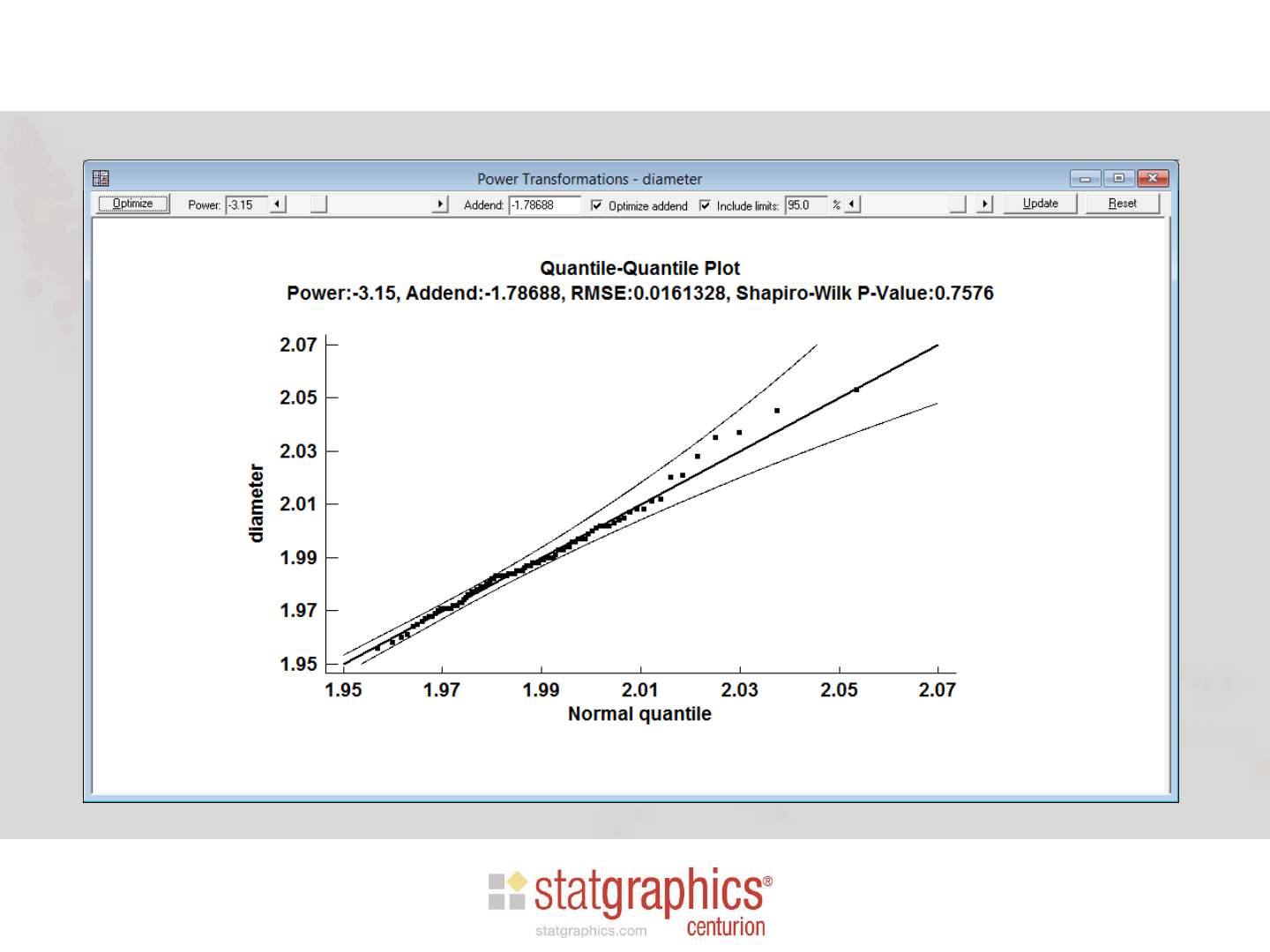
Power plus Addend
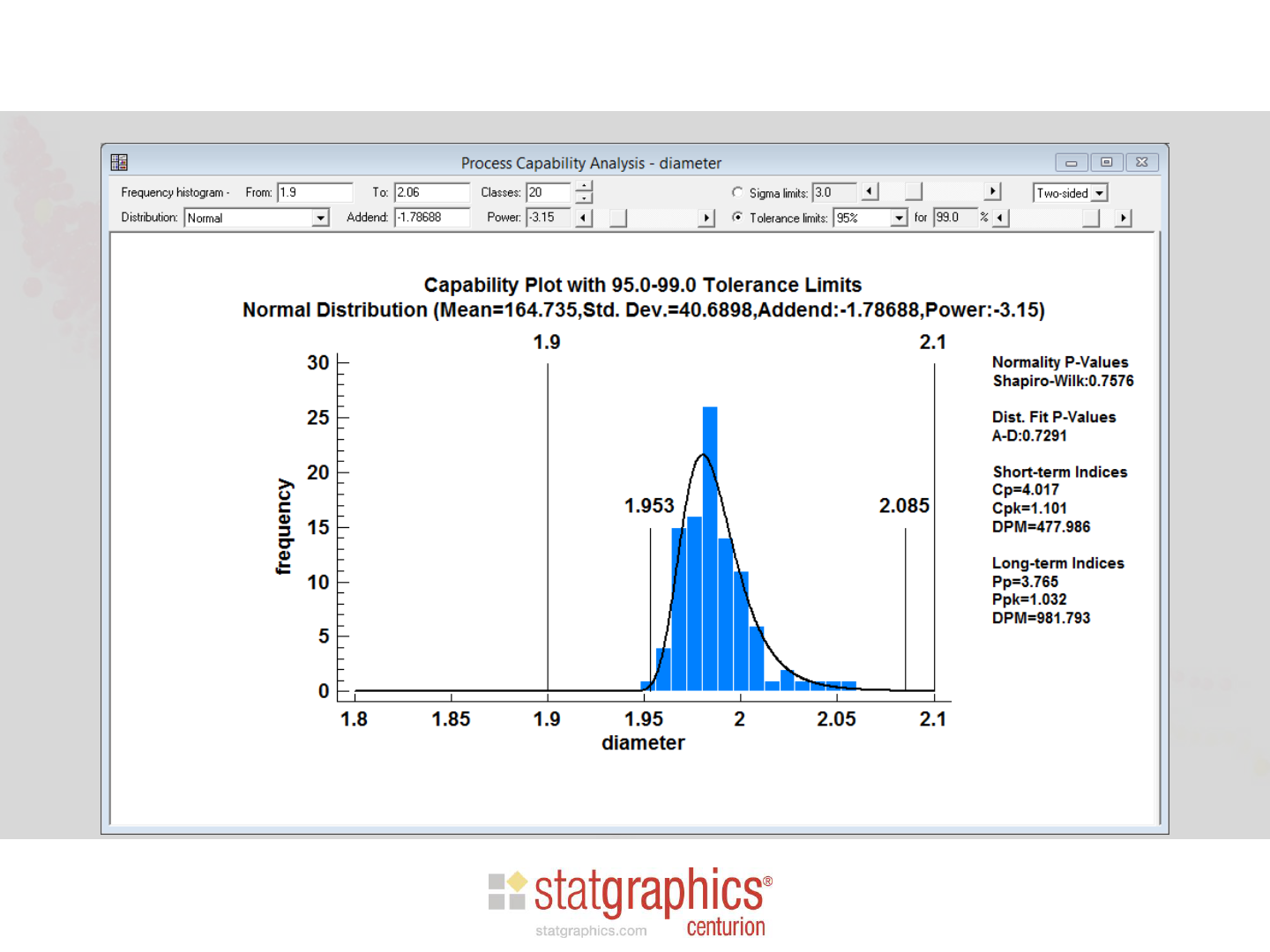
Tolerance Limits

Step 3: Find an Alternative Distribution
• Statgraphics will calculate statistical tolerance limits
for the following distributions:
• Normal
• Lognormal
• Weibull
• Cauchy
• Exponential
• 2-parameter exponential
• Gamma
• Laplace
• Largest extreme value
• Pareto
• Smallest extreme value

Distribution Fitting
• Comparison of alternative distributions
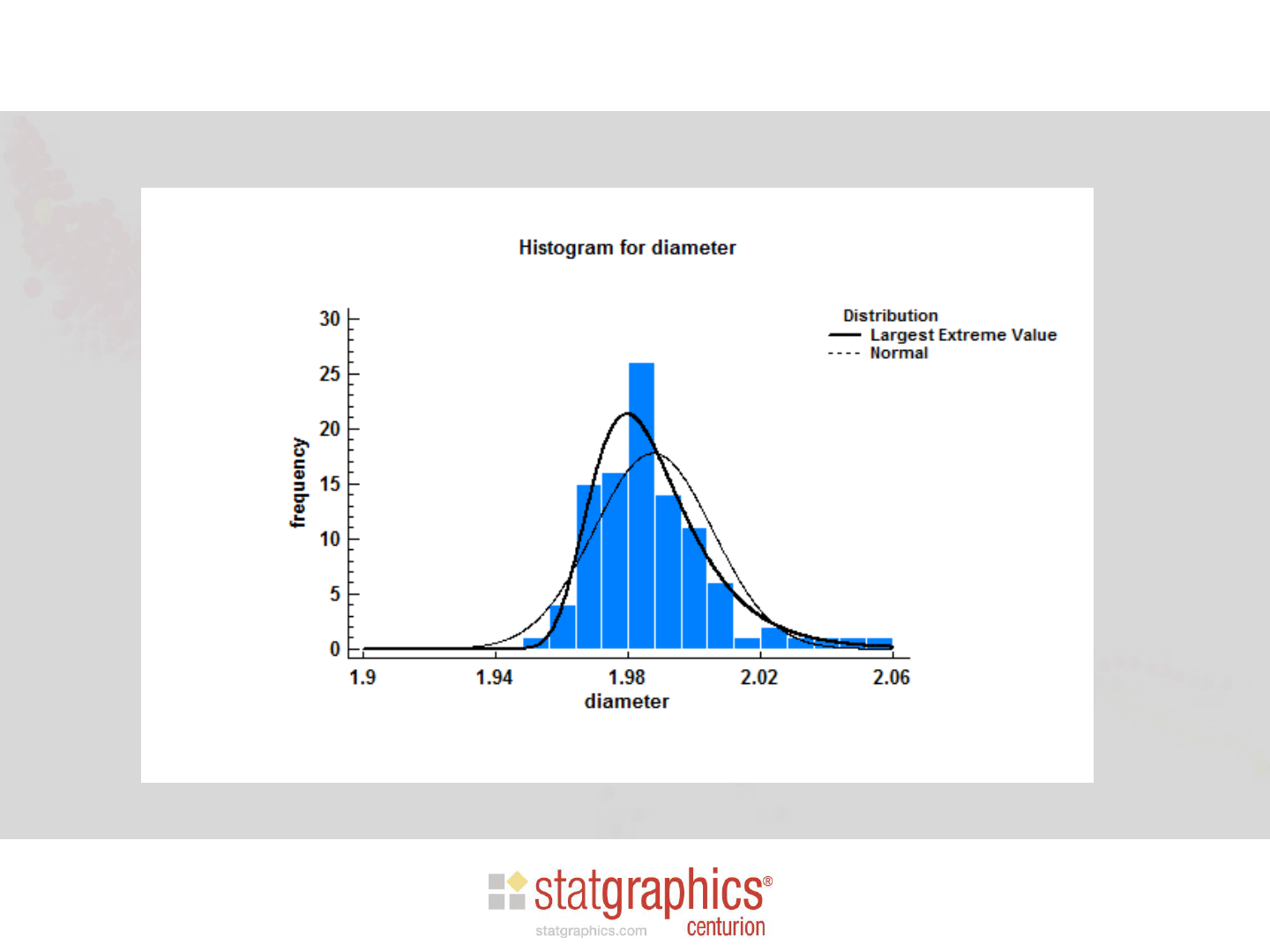
Fitted Distributions

Goodness-of-Fit
• To test goodness-of-fit for alternative
distributions, Anderson-Darling test is popular.
• Be sure to use “modified” form of the test, which
adjusts the test statistics and P-value to account
for estimated parameters.

Tolerance Limits
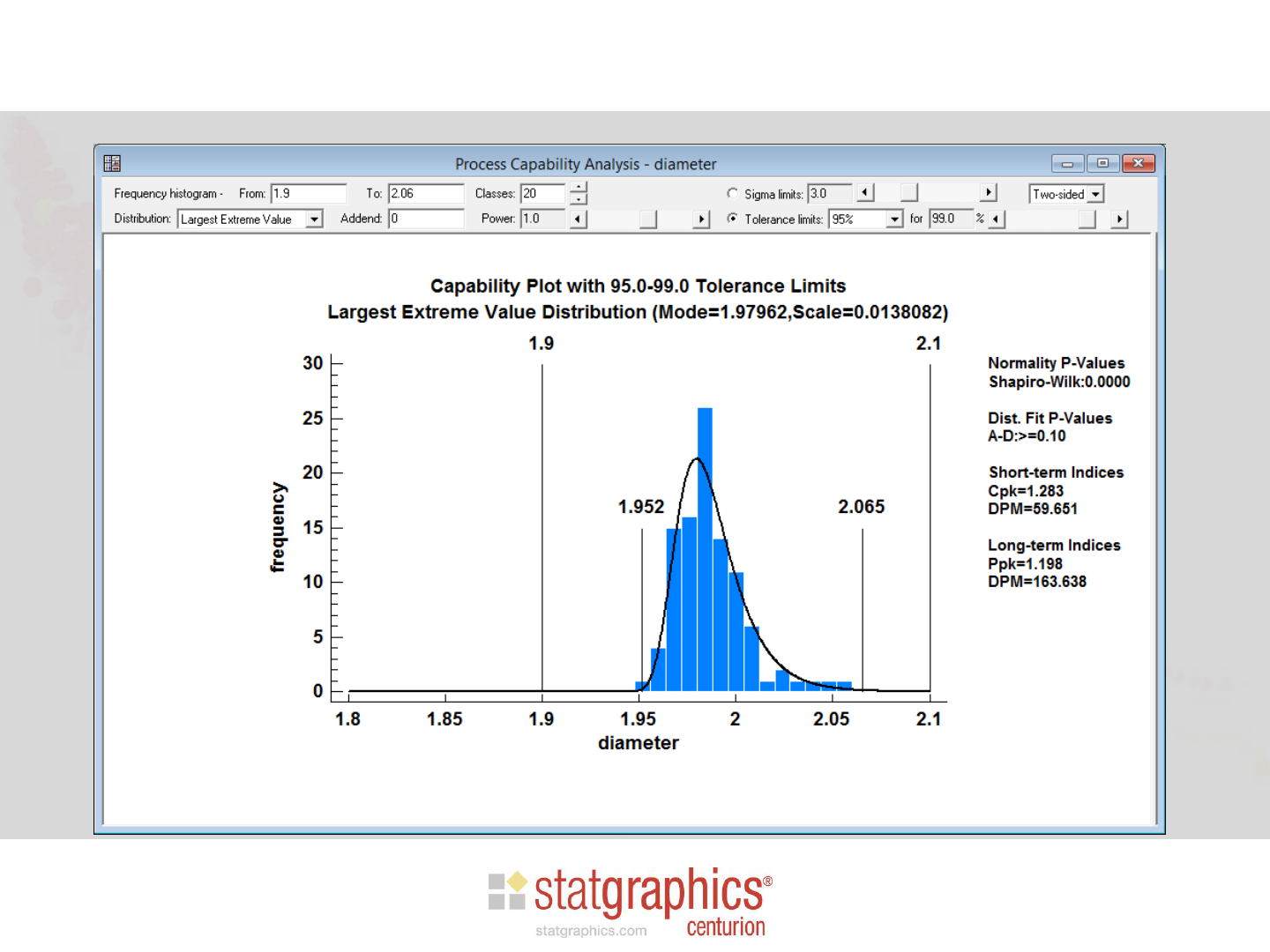
Tolerance Limits

Step 4: Nonparametric Limits
• Can specify either the population percentage or
the confidence level, but not both.
• Tolerance interval is [ X
(d)
, X
(n-d+1)
]
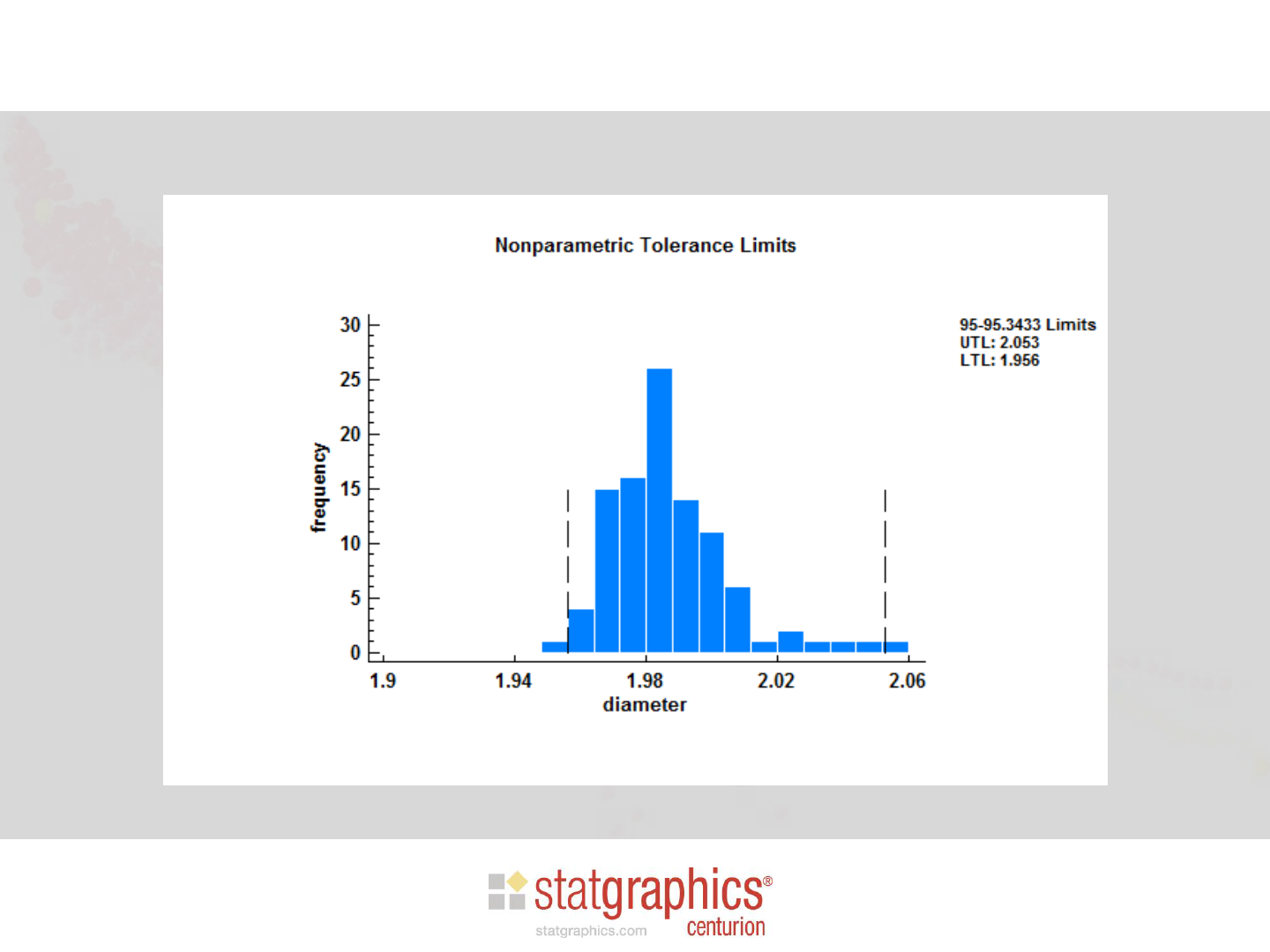
Nonparametric Limits

Sample Size Determination –
Nonparametric Limits
• How large a sample is needed so that the range
[min, max] forms a 95-99 tolerance interval?

Sample Size Determination –
Parametric Limits
• How large should n be when fitting a normal or
some other distribution?
• Different approaches to the problem.
1. Choose n so that the probability of including
P*% or more of the population in the
tolerance interval is small, where P* > P.
2. Choose n so that the probability of the entire
tolerance interval being within the
specification limits is large.

Example: LEV Distribution
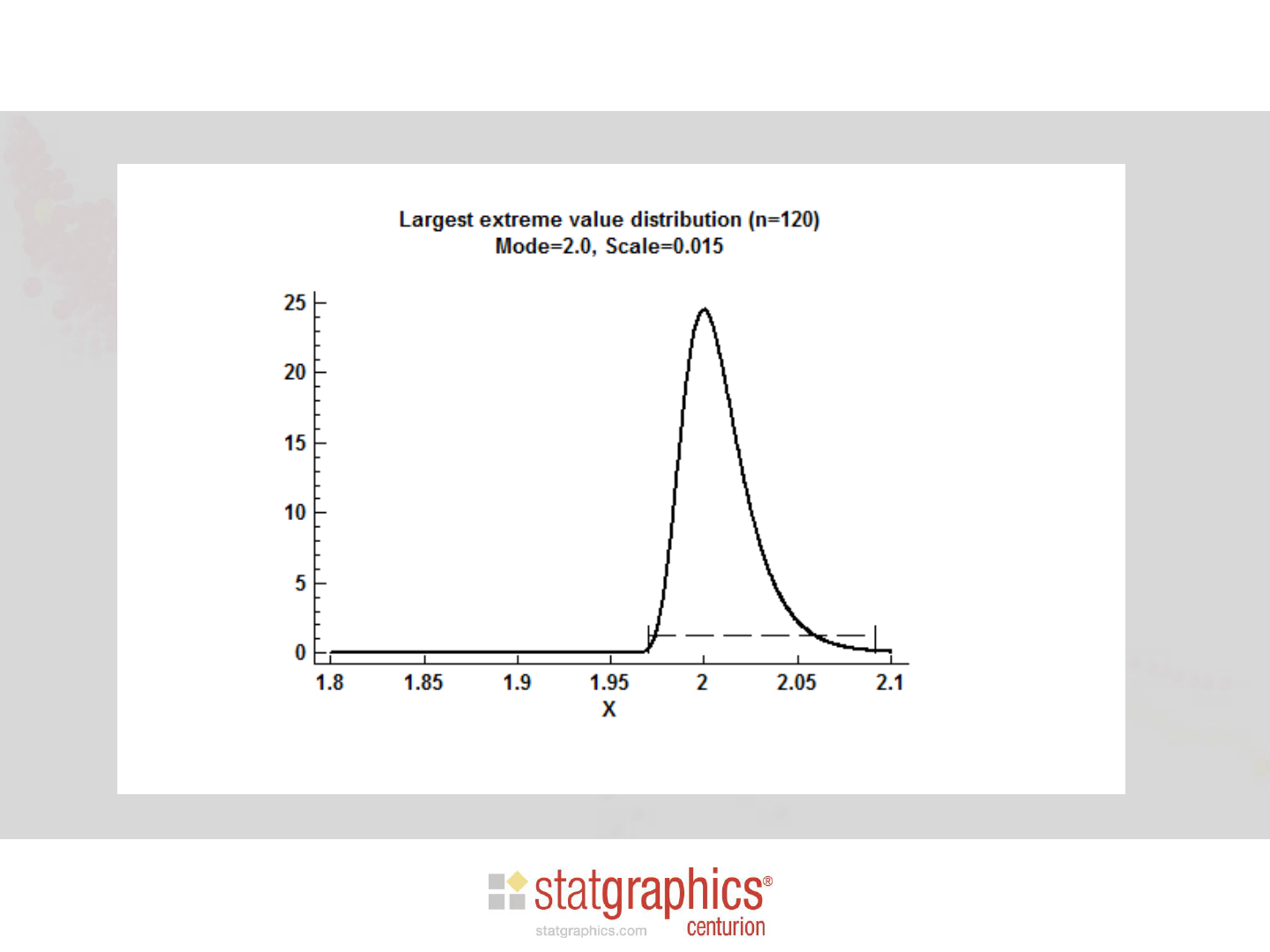
Requires n=120 Observations
System Preferences

